[Closed] measuring pi

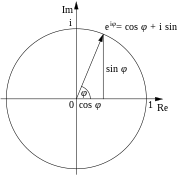
Don't they use a trig formula or similar and an algorithm?

[img] [/img]
[img] [/img]

Basically they draw an enormous circle and use a really accurate ruler. That way, when dividing the circumference by the diameter any innaccuracies in the measurements are essentially nullified.

[url= http://en.wikipedia.org/wiki/Gauss%E2%80%93Legendre_algorithm ]Gauss–Legendre algorithm[/url]

http://en.wikipedia.org/wiki/Pi

I remember working Pi to over 10,000 places for a school project many years ago. I actually got the computer to do it, I wrote a program that placed random dots on a square, and counted how many were inside the circle and outside, AKA [url= http://learntofish.wordpress.com/2010/10/13/calculating-pi-with-the-monte-carlo-method/ ]Monte Carlo Method[/url].. After a few days it had calculated Pi to a lot of decimal places.

So Pi [url= http://en.wikipedia.org/wiki/Proof_that_22/7_exceeds_%CF%80 ]does not equal 22/7?[/url] well everyday is an education

Anyone else read contact? Love the ending, with the message encoded deep in the solution for Pi.

Anyone else read contact? Love the ending, with the message encoded deep in the solution for Pi.

Not yet. Worth reading?

[img] [/img]

[img] [/img]

Anyone else read contact? Love the ending, with the message encoded deep in the solution for Pi.
Not yet. Worth reading?

Way better than the film imho. And I liked the film... 🙂

Not yet. Worth reading?

Yes definitely, the book is fabulous and a much more complete story than the film, which I also liked as beanum's comments.

I know you shouldn't compare two mediums, but there is so much more to enjoy in the book especially the way Sagan blends real science with fiction. He leaves you wanting to read more about the subject.

Good book indeed.

Pi can be calculated with a formula that's based on radians and the value of pi - it's a recursive type formula so the more times you loop through it the more decimal places you calculate down to.

There's quite a few ways of doing it, I had to do it for some coursework back in college, think I used the fact that 4*arctan(1) = pi, so if you can find an estimate for arctan(1) then you've got it. The first way that springs to mind to do that would be to find the root of tan(x/4)-1, which is simple (graph paper, a very sharp pencil, and a magnifying glass - sorted).

https://www.google.co.uk/search?q=tan%28x%2F4%29-1&ie=utf-8&oe=utf-8&aq=t&rls=org.mozilla:en-GB:official&client=firefox-a

A better question, and one I always keep forgetting to ask people who might know, is why? Why does anyone want/need to know any more then 15 digits or so? Even space shuttles and such don't need to be that accurate (I think). So why on earth are we putting super computers to work finding several billion digits of an irrational number - what are we expecting to find? A message from god?

Exactly 🙂 I'm sure there are people who reckon that Contact could just be a case of fiction reflecting the truth...

Also something interesting is the proof that pi is actually irrational. Bit more complicated than proving various surds are irrational.

http://en.wikipedia.org/wiki/Proof_that_%CF%80_is_irrational

Why does anyone want/need to know any more then 15 digits or so?

Using computers to estimate an irrational number to as many places as you possibly can is in no way pure mathematics.

Pffft, who am I kidding? Maths undergrads in a social situation?!

Ridiculous 🙂

Using computers to estimate an irrational number to as many places as you possibly can is in no way pure mathematics.

Thanks, I'll give it a go 🙂

There must be some practical application of knowing values of irrational numbers to increasingly long decimal places?

Like the way that extremely large prime numbers are valuable in cryptography for instance.

Oh and 'maths undergrad in can't spell '[i]pursuit[/i]' shocker' 😀

If there is one thing I would change with a magic wand about myself (well apart from 'that') it would be to be excellent at maths. I have tried in adult life to re-learn and get better, but it just wasn't happening.

EDIT - just thinking about it, if you had values of Pi and 'e' to decimal places longer than anyone else, then when you factored them wouldn't that also be valuable in cryptography?

Indeed, it's all a bit dirty, isn't it? Still - it looks like the digits are random. Allegedly there is no proof that they are or should be - so let's find out.

Personally I'm annoyed that I can remember the first 4 decimal places of it, what a waste of my memory.

What are they expecting to find? The Fibonacci sequence or something? Just seems like such a waste of time.

EDIT - just thinking about it, if you had values of Pi and 'e' to decimal places longer than anyone else, then when you factored them wouldn't that also be valuable in cryptography?

I don't really know much about crypotgraphy (but that will change soonish), but how do you factor a decimal number? Unless you multiply whatever number you've got after truncating it by 10^n in order to make it an integer, but then you've just got a really big number, which is probably not going to be prime.

Unless you multiply whatever number you've got after truncating it by 10^n in order to make it an integer,

I think I better stay out of it and refer you to the earlier question of what the practical application of knowing Pi to very long decimal places might be.

I'm a bit out of my depth otherwise.

I might even have misunderstood what factoring means. I thought it just meant multiplying! 😳