[Closed] calculate surface area of a curved roof

That's not a lot of info.

Is it barrel shaped? A mound? Conical?

If it's a regular arc, ie you could continue it to make a whole circle, it's relatively straightforward.

You just draw out that circle, measure the diameter, then use pi to calculate the circumference, and a protractor to work out what proportion of that circumference covers your arc.

If it's a circular profile, don't you just need the radius and how much of the circle you've got?

EDIT: beaten to it.

looks like this

[img] [/img]

The length of the arc is 54.017m, giving you an area of 1242.3sqm (i think 😛 )

how did you get to that yorkshire89?

teach me how to fish ( and measure a curved roof)

I cheated with CAD 8)
It does assume the arc has the same radius along the full length though.

You could do the same on paper, draw a line 480mm, then another from the centre 106mm (wall height). Use a pair of compasses to draw the arc and overlay it with a piece of string.

send me the cad file? 😀

Would it actually be a bit of a circle? More likely to be a parabola innit?

Looks very slightly parabolic to me.

yeah it's not the same radius along its length

Excuse my scribbles but i believe...

[img] [/img]

Re parabola given the info you have it will always solve circular. The maths is quite hard for elliptical curves even with additional info...

Email on it's way. If you can get some more heights at regular intervals you should be able to get it a little more accurate 🙂

Are you left-handed? (-:

Ah bugger i missed a 2 when i expanded my ry^2 too in fact I've expanded all wrong. 0 marks for me.

you fool dangeourbrain! only kidding, many thanks. I am after an estimate really and I had done something in sketchup. Was joking about the email but i got it!

ta muchly all, a nice friday puzzle

I don't have a calculator to hand and my memory of trigonometry is rusty, but it looks like basic trig:

1. an imaginery straight line (A) from the edge of the roof at the ground to the apex, gives a right angled triangle (other two sides are ground to apex vertically and half the ground length, and they are known).

2. use pythagorus to calculate A.

3. calculate angle at which A and the ground to apex line meet (opposite over adjacent equals hypotenuse?)

4. the radius can be calculated then, because it's a line from the centre of the circle to the middle of A, so another right angled triangle with A/2 as one length, and you have the angle needed from step 2.

5. Once you have the radius, you can calculate the circumference with 2 x Pi x R.

6. Ground length and the radius can then be used to calculate angle between lines drawn from either end of the building to the centre of the circle (again 2 right angled triangles).

7. ratio of angle to 360 degrees gives the length of roof as a ratio of the circumference.

8. Multiply by width of roof for area.

Easier to explain and understand if you draw it on paper.

Must try harder

[img] [/img]

Probably still wrong mind...

I'm making assumptions here in that the curve you describe follows the trace of a much larger circle, like below:
[img] 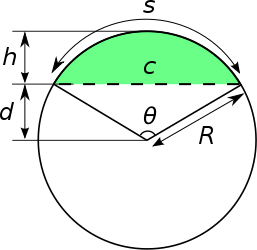[/img]

Taken from [url= https://en.m.wikipedia.org/wiki/Circular_segment ]here[/url].

R = h + d = h/2 + c²/8h = 32.470m

Now we know R, we can use the cosine rule to figure out the central angle [i]theta[/i] = 95.318°

From this:

s = angle°/180° * ?R = 54.017m

Multiply this by the other length and you have a roof area of 1242.393m²

But don't take my word for it. I'm just off nightshift.

@dangeourbrain what is the answer then... 😆

That doesn't look circular, or parabolic to me.....

Depending on how easy it is to measure to the ceiling height and how accurate you need to be, I would go old school & measure the height at various position across the width of the building.

E.g. measure height of roof every 5 metres in from the edge to the centre.
Use graph paper (or preferably someone with CAD) to plot the positions and draw a curve through the points.
Measure the length of the resulting line & multiply by 2 (because you only measure to the centre of the room) and then multiply that by the length of the room.

Can't you just run a metre wheel along the edge of the roof and multiply that length by the width of it?

For excel then...

Where width is a1, height b1 length c1...

R
=((a1/2)^2+b1^2)/2*b1
= 32m
Assuming r is a2
Alpha
=degrees(asin((a1/2)/a2))
=95
Alpha as a3...
C
=(4*a3*pi()*a2)/360
=54m
C as a4
Area
=C1xa4
=1243m approx.

nickjb - Member
Would it actually be a bit of a circle? More likely to be a parabola innit?

POSTED 42 MINUTES AGO # REPORT-POST
martinhutch - Member
Looks very slightly parabolic to me.

POSTED 41 MINUTES AGO # REPORT-POST
howsyourdad1 - Member
yeah it's not the same radius along its length

I agree it looks like that, but wideangle lenses distort so much, it's impossible to tell from the photo.

Exhibit A. skewiff parabolic rainbow:

[img] ?zz=1[/img]

Does it need to be perfect or rough?

Can you measure the height in a number of places to get a feel for what the curve is like

Looks newish. Phone up the planning department and get the drawings from the application!

I'd chuck a rope over it mark both ends where the roof ends remove rope and measure distance between marks. 🙂

Make a strava segment over it 😀

Measure the height every meter. Ensure you measure the highest point also. Sketch it to scale on graph paper. Measure the resulting arc and multiply by your scale to give the value in meters. Multiply that by the length of the roof.

Also in my experience, architects only occasionally plan things to be other than circular (or sectional) largely as its very very hard to form most things to anything other than a circular curve, because of the amount of data you need. When they are other than, they tend to be concurrent circular sections r=a arc x degrees, r=b arc y degrees, r=c arc z degrees. Plotting loci isn't too bad given the equation but actually making that on an industrial scale is seriously difficult and correspondingly expensive so tends to be reserved for flagship buildings (or first drafts). It's not so difficult in brick etc which you can cut to suit a form but the windows look to follow the roofline and unless they're timber (steamed and bent on site) they're going to be box section formed with pressure rolls which tend to excerpt constant pressure along the length producing a constant curvature, accurately varying that is difficult and tends to result in stepping where the radius changes.

My money is on circular ish, possibly 2 variant radii, 1 for peak and 1 sides

Looks newish. Phone up the planning department and get the drawings from the application!

it's from the 1970s. In Sweden. I am the planning department, well kind of, I work with them alot!

😀

Newish for us, old hat for the Swedes.

Trapeziums

Does [url= http://keisan.casio.com/has10/SpecExec.cgi?id=system/2006/1223291032 ]this [/url]help?

My solution:

1. lick index finger.
2. hold index finger above head in air for a moment.
3. come up with a simple height x length calculation, and add how much my wet finger in the air suggested (@10% would be right).
4. add 10%, just in case.
5. Submit quote on back of fag packet.

30% contingency here.

I'm going to revise my rope method and use string instead as a much better medium for guessing the length of something unknown. Photograph end of building square on with camera level. Measure length of string needed to follow roof line and length of string to follow known building width and calculate distance over the roof from that.

This will also mean you know the length of a piece of string which could come in handy as it's something few people seem to know and are always asking.

If you look at the building, the maximum slope of the roof is ... what .. 30 degrees?
So the maximum possible slopeline length ignoring the height of the building is 48/(cos30) = 55m.
The minimum possible slopeline length is sqrt (10^2 +48^2) = 50.
Scientific answer = 52.5m

It looks like the building is roofed with corrugated iron.

Count the sheets of iron. They have a known dimension and area, and allowing for the overlap, just multiply the area of one sheet by the number of sheets.

I went through this process about 30 years ago. I had a similar building, vaguely parabolic roof that I wanted painted. I did a few calculations myself. When I contacted the painter, he came out, walked along the building and gave me a price without writing any notes or calculations.

So I asked him how he did it. He looked at me as if I was stupid, and said "Well there's x amount of sheets, and it's $y dollars to paint a sheet, so the total is $yx". And I did feel stupid. 🙂

Are those verge sections the same length? Count them x unit length in metres x 23m

My solution would be to buy loads more tiles than you need from B&Q because they give you 45 days to take them back.