So there's the familiar problem that has been around for quite a while now, but personally, I have never been able to get my head around WHY the answer is the case. I've seen it written out long ways, short ways, with demonstrations and thought experiments, but never have I been able to bend my mind to accept it.
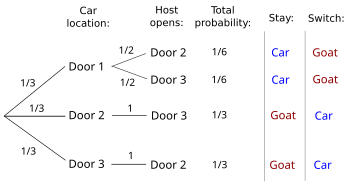
Problem (in this version, from Wired magazine):
Suppose you're on a game show and you're given the choice of three doors: Behind one door is a car; behind the others, goats. You pick a door, say Number 1. The host, who knows what's behind all the doors, opens another; say Number 3, which he knows is hiding a goat. He then asks, "Do you want to pick door Number 2?" Is it to your advantage to switch your choice?
Answer:
Yes. Switching your choice always raises your odds. Originally you had a 1 in 3 chance of guessing the correct door. When Monty shows you the goat behind a door you didn't choose, the probability of a car being behind that door drops to zero and the chance that there's a car behind the third door thus rises to 2 in 3. So your odds improve if you switch your choice.
Now, here is where I can't follow it. Why are the odds after the door has been opened not 1 in 2?
The way I see it, when you are offered the swap, you are effectively given the choice to choose again, between the two remaining doors, which makes it 1 in 2 (surely?). If you choose the same door again, it is the same effect as sticking with the original 1 in 3 odds, but with updated information - making it a 1 in 2. The third door is now irrelevant, which suggests to me that 'the chance that there's a car behind the third door thus rises to 2 in 3.' is bunkem.
Anyone care to have a go at explaining it?
